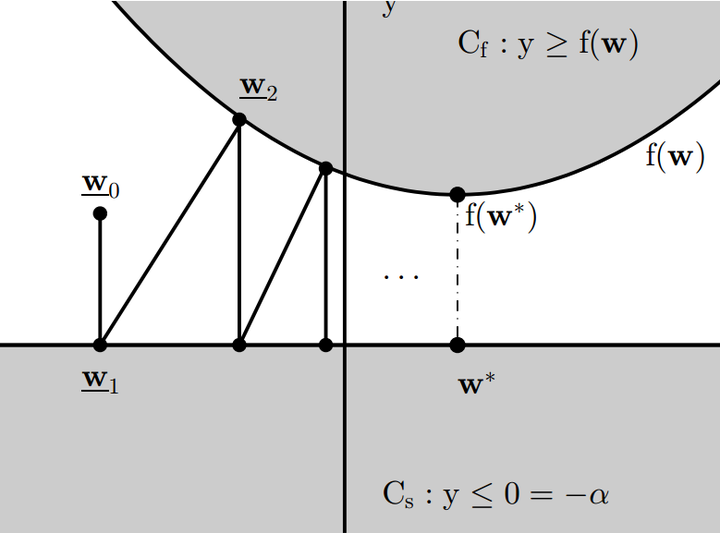
 Optimization steps
Optimization steps
Abstract
A new optimization technique based on the projections onto convex space (POCS) framework for solving convex and some non-convex optimization problems are presented. The dimension of the minimization problem is lifted by one and sets corresponding to the cost function are defined. If the cost function is a convex function in $R^N$ the corresponding set which is the epigraph of the cost function is also a convex set in $R^{N+1}$. The iterative optimization approach starts with an arbitrary initial estimate in $R^{N+1}$ and an orthogonal projection is performed onto one of the sets in a sequential manner at each step of the optimization problem. The method provides globally optimal solutions in total-variation, filtered variation, $\ell_1$, and entropic cost functions. It is also experimentally observed that cost functions based on $\ell_p$; $p \leq 1$ may be handled by using the supporting hyperplane concept. The new POCS based method can be used in image deblurring, restoration and compressive sensing problems.